12.1 – The interaction of matter with radiation
Photons and the wave-particle duality of light
For a long time, it was believed that light was simply a wave. However, Einstein’s nobel-prize winning explanation of the photoelectric effect created a new definition for the behaviour of light; it could be a both a wave, and a particle at the same time. This phenomenon is called the wave-particle duality.
The Photoelectric Effect
The photoelectric effect was discovered when shining light on certain metals seemed to cause electron emission. In the photoelectric experiment, the emitted electrons can be passed through a circuit, which allows us to measure the electron flow.
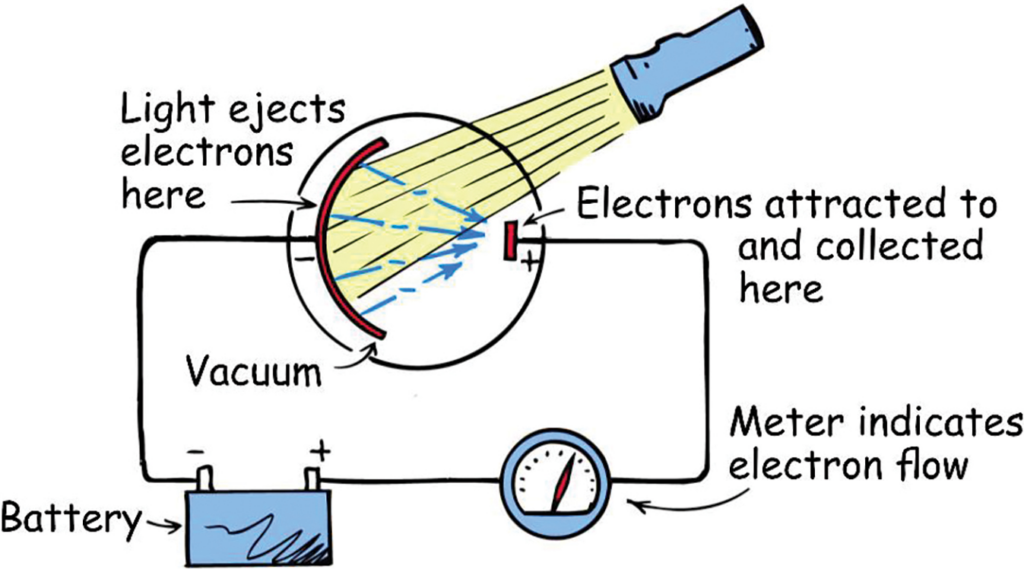
Observations from the photoelectric effect:
- There is a minimum frequency for which electrons can be emitted, called the threshold frequency (f0).
Light behaves like a particle, called a photon, and it’s energy is given by E=hf.
A certain amount of energy is needed for an electron to escape the nucleus of the atom, this is energy is called the work function (Φ).
Below the threshold frequency, the photon has less energy than the work function, and therefore cannot release the electron.
- Increasing the intensity of light only increases the number of electrons emitted. If the frequency is below the threshold frequency, then no electrons are emitted no matter the intensity of the light.
Increasing the intensity of light simply increases the number of photons incident per second, therefore more electrons are emitted. In the case that the frequency is below the threshold frequency, then no electrons can be emitted regardless of the intensity.
- Low intensities of light will still emit electrons if the frequency is high enough.
If you throw a single photon onto the plate, it will emit a single electron, as long as the frequency is above the minimum threshold.
- If the photons first pass through a glass panel before reaching the metal plate, no electrons are emitted.
Glass absorbs all the high energy light, and only lets the low energy photons pass onto the metal surface, thus no electrons are emitted.
Through the following statements Einstein concluded that light was also a particle:
- Light behaves like a particle (the photon) when absorbed or emitted.
- The energy of the light is given by its frequency and plank’s constant, E=hf
- A single photon can only interact with one electron.
- A certain amount of energy is needed for an electron to escape the nucleus of the atom, this is energy is called the work function (Φ).
- Any excess energy provided by the photon turns into the kinetic energy of the emitted electron, given by E = hf – Φ
Matter waves
Louis de Broglie suggested that if waves could behave like particles, then matter must also possess some wave-like properties. He proposed the wavelength λ is associated with its momentum p, given by the De Broglie equation:
$$\lambda = \frac{h}{p}$$
In 1925, de Broglie’s hypothesis was proven correct when experiments showed that electrons (which have mass) could show interference patterns.
Pair production and pair annihilation
Pair annihilation: When a particle meets its antiparticle, they annihilate and release energy equivalent to the total mass-energy of the two particles.
Pair production: When a particle and its antiparticle materialize from a photon. The photon’s energy must be at least the mass of the two particles.
Quantization of angular momentum in the Bohr model for hydrogen
Bohr developed a model of the atom that could explain the emission and absorption spectra of hydrogen. His model proposed that electrons orbit the nucleus through discrete orbital paths, defined by fitting closed standing waves along the electron orbit.
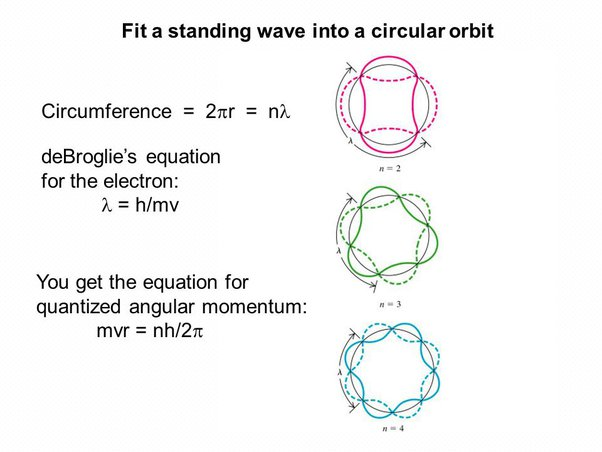
Schrodinger’s wave function
The the quantum world, particles exist in a state of probabilities, until observed. The wave function tells us the probability P(r) of finding a particle inside the volume V at that time.
$$P(r)=|\psi|^{2}\triangle V$$
Heisenberg’s Uncertainty Principle
The uncertainty principle states that you cannot know a particle’s exact position x and momentum p at the same time. The more precisely you know the value of one, the more uncertain the other becomes.
$$\triangle x \triangle p \geq \frac{h}{4\pi}$$
The same principle applies to the energy E of a particle, and the lifetime t of that energy state. In other words, if the lifetime is very short, then its energy is unknown.
$$\triangle E \triangle t \geq \frac{h}{4\pi}$$
Quantum Tunneling
Believe it or not, there is a non-zero chance of you walking into a wall, and appearing on the other side. This is because when a particle approaches a barrier, it will have a certain probability of existing on the other side of that barrier. This phenomenon is called quantum tunneling.
The probability for a particle to pass through a barrier is affected by two things: It’s mass, and the width of the barrier. Increase the mass, or the width of the barrier, and you reduce the probability of quantum tunneling.
This is why there is a very small chance for a human to quantum tunnel, but in the quantum world, it happens quite often.
12.2 – Nuclear Physics
➔ Rutherford scattering and nuclear radius
➔ Nuclear energy levels
➔ The neutrino
➔ The law of radioactive decay and the decay
constant
