2.1 – Motion

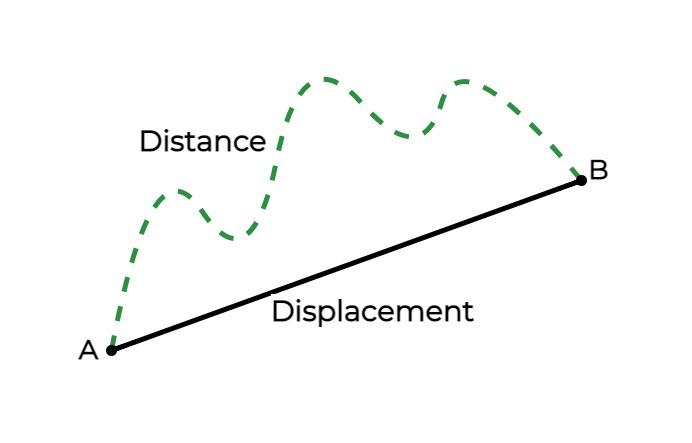
Distance and displacement

Distance (Scalar): The total length of the path traveled by an object

Displacement (Vector): The length between the start and end position of an object

Speed and velocity

Speed (Scalar): The rate of change of distance, or the distance divided by the time taken.

Velocity (Vector): The rate of change of displacement in a given direction, or the displacement divided by the time taken.

Acceleration

Acceleration (Vector): The rate of change of velocity, calculated by dividing the change in velocity by the time interval. Acceleration can be positive (speeding up), negative (slowing down), or zero (constant velocity).

Graphs describing motion

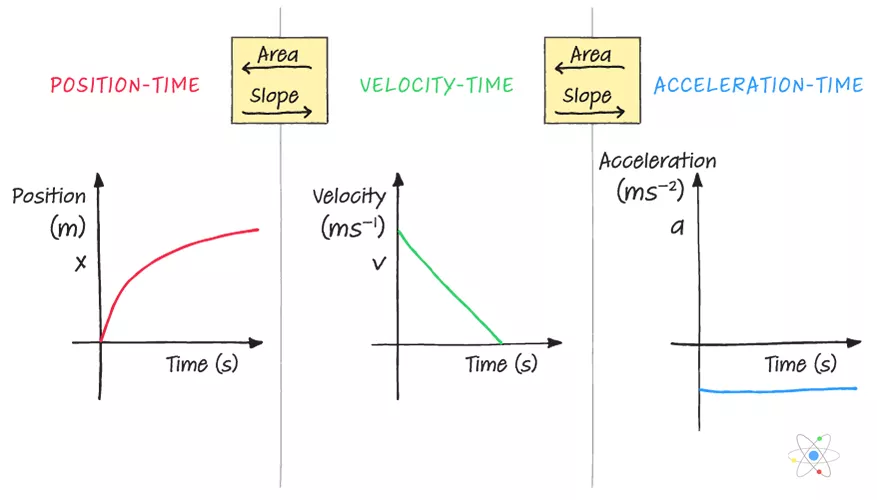
Distance-time graphs show how the distance or displacement of an object changes with time.

Velocity-time graphs illustrate how the velocity of an object changes over time. The area of the graph is the distance travelled.

Acceleration-time graphs display how the acceleration of an object varies with time. The area under the graph is the average velocity.

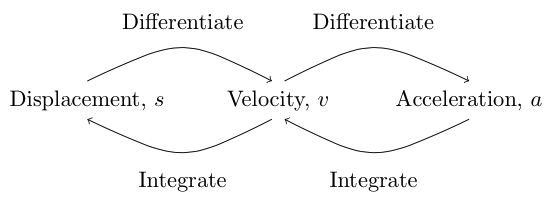
Equations of motion for uniform acceleration

The SUVAT equations are a set of equations that can be used only when acceleration is constant (such as the acceleration due to gravity).

$$v = u + at$$

$$s = ut + \frac{1}{2}at^2$$

$$v^2 = u^2 + 2as$$

$$s = \frac{(v +u)t}{2}$$

v = final velocity, u = initial velocity, t = time taken, s = displacement, a = acceleration

Projectile motion

Projectile motion refers to the motion of an object that is launched into the air and moves under the influence of gravity.

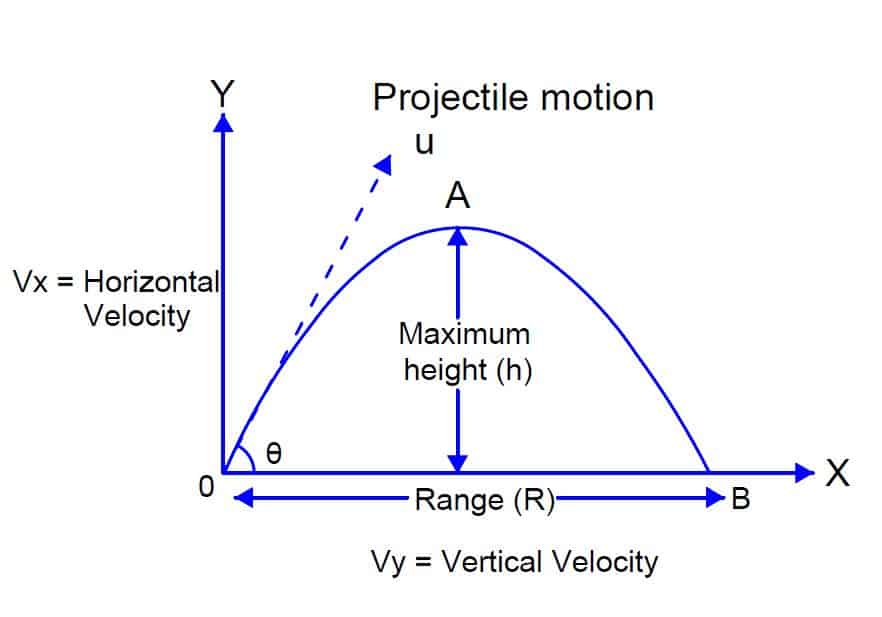
• The horizontal component of the velocity remains constant
• The vertical component is affected by the force of gravity
• The maximum height is reached when vertical velocity is zero

Exam Tip!
In Mathematics, you learn that the range of a function is through the y-axis. In projectile motion, range is in the x-axis. It is easy to get these mixed up!

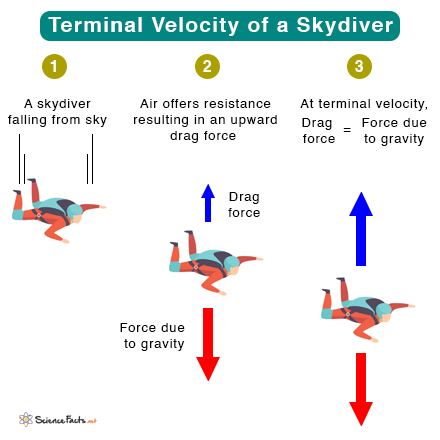
Fluid resistance and terminal speed

When the drag force is equal to the force of gravity on a falling object, the object stops accelerating and reaches terminal speed.

2.2 – Forces

Objects as point particles

In some cases, objects can be treated as point particles that have mass but negligible size. This simplification allows us to focus on the object’s motion without considering its size or shape.

Free-body diagrams

Free body diagrams allow us to analyze all the forces acting on an object. These diagrams show all the forces acting on the object as arrows, indicating both their direction and magnitude. Even if an object is not moving, there may still be forces acting on it

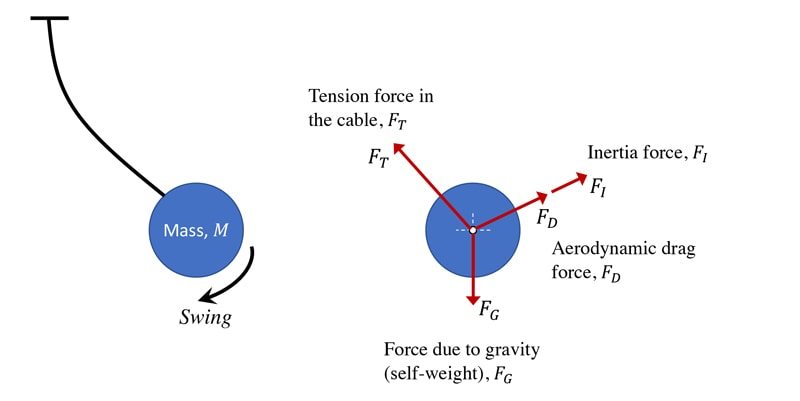
To determine the resultant force:

• Using trigonometry, resolve foces into horizontal and vertical components
• Add up the horizontal components
• Add up the vertical components
• Use the sum of components to find the magnitude and direction of the resultant force

Translational equilibrium

An object is in translational equilibrium when the vector sum of all the forces acting on it is zero. The forces cancel each other out, resulting in no net force on the object.

Newton’s laws of motion

Newton’s laws of motion form the foundation of classical mechanics. They describe how forces affect the motion of objects.

• Newton’s First Law (Law of Inertia): An object at rest will remain at rest, and an object in motion will continue to move at a constant velocity unless acted upon by an external force.
• Newton’s Second Law: F = ma
• Newton’s Third Law states that for every action, there is an equal and opposite reaction.

Friction

Friction is a force that opposes the relative motion between two surfaces in contact. It arises due to the microscopic irregularities of the surfaces.

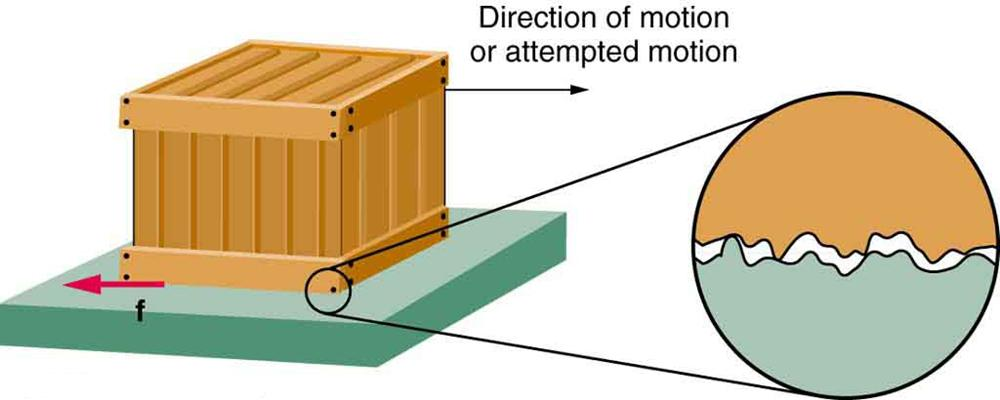
Friction can be static (stops object from moving) or kinetic (slows down a moving object).

Static friction is larger than kinetic friction because it takes more work to start an objects motion, than when it is already moving.

2.3 – Work, energy, and power

Principle of conservation of energy

Energy cannot be created or destroyed but can only be transformed from one form to another. In other words, the total energy of a closed system remains constant over time.

Kinetic energy

The energy carried by an object due to its motion. It depends on the mass of the object and its velocity.

$$E_{K} = \frac{1}{2}mv^2$$

Exam Tip!
Memorizing the kinetic energy equation will save you some much-needed time in an exam, since it is so often used by every chapter.

Gravitational potential energy

The energy carried by an object due to its position in a gravitational field. It depends on the height and mass of the object.

$$\triangleE_{p} = mgh$$

Where m is the mass, g is the acceleration due to gravity, and h is the height.

Elastic potential energy

The energy stored in a stretched or compressed elastic object, such as a spring.

$$E_{P} = \frac{1}{2}k\triangle x^2$$

Where k is the spring constant and x is the displacement.

Work done as energy transfer

Work is done is a measure of energy transfer when a force is applied to an object.

when a force is applied to an object, causing it to move in the direction of the force. It can be expressed as

$$W = Fs cosθ$$

Where F is the force, d is the displacement, and θ is the angle between the force and displacement vectors.

Power as rate of energy transfer

Power is the rate at which work is done or energy is transferred. It measures how quickly energy is converted or transferred. Power (P) is calculated by dividing the work done (W) by the time taken (t), and it can be expressed as P = W/t.

Efficiency

Efficiency is a measure of how effectively energy is converted from one form to another. It is the ratio of useful energy output to the total energy input, expressed as a percentage. Efficiency is an important consideration in various energy conversion processes.

Gravitational potential energy

Gravitational potential energy is the energy possessed by an object due to its position in a gravitational field. It depends on the height and mass of the object. The gravitational potential energy (PE) of an object near the surface of the Earth is given by the equation PE = mgh, where m is the mass, g is the acceleration due to gravity, and h is the height.

Elastic potential energy

Elastic potential energy is the energy stored in a stretched or compressed elastic object, such as a spring. It depends on the spring constant and the displacement from the equilibrium position. The elastic potential energy (PE) of a spring is given by the equation PE = ½kx², where k is the spring constant and x is the displacement.

Work done as energy transfer

Work is done when a force is applied to an object, causing it to move in the direction of the force. The work done (W) is equal to the force multiplied by the displacement and the cosine of the angle between them. It can be expressed as W = Fdcosθ, where F is the force, d is the displacement, and θ is the angle between the force and displacement vectors.

Power as rate of energy transfer

Power is the rate at which work is done or energy is transferred. It measures how quickly energy is converted or transferred. Power (P) is calculated by dividing the work done (W) by the time taken (t), and it can be expressed as P = W/t.

Efficiency

Efficiency is a measure of how effectively energy is converted from one form to another. It is the ratio of useful energy output to the total energy input, expressed as a percentage. Efficiency is an important consideration in various energy conversion processes.

By understanding the concepts of work, energy, and power, we can analyze and quantify the transfer and transformation of energy in various systems and processes.